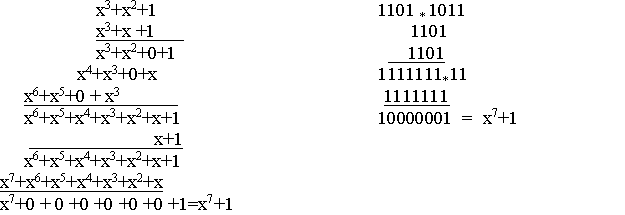
Циклическими
кодами
называют специальную группу кодов, для
построения которых могут быть использованы
циклические свойства квадратных матриц, а
также коды, которые описываются
неприводимыми, образующими (порождающими)
многочленами (полиномами). Например, для
кодовой комбинации 101101 полиномиальное
представление таково:
A(X)
= 1×x5
+ 0×x4
+ 1×x3
+ 1×x2
+ 0×x1
+ 1 = x5 + x3 + x2 + 1.
Циклические
коды относятся к систематическим (n,
k)
кодам, в которых контрольные r
и информационные k
разряды расположены на строго определенных
местах: n
= k
+ r.
Рассмотрим алгебру циклических кодов. Допустим, необходимо перемножить три многочлена (x3+x2+1)·(x3+x+1)·(x+1). Действия производятся также как в обычной алгебре, только сложение проводится по модулю 2.
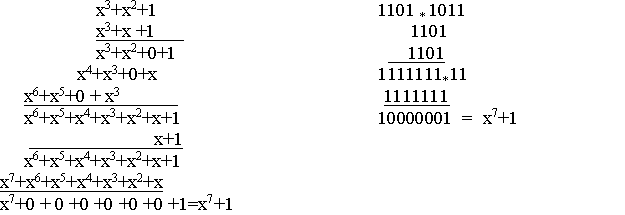
При
делении операция вычитания заменяется
операцией сложения по модулю 2. Например,
необходимо разделить многочлен седьмой
степени на многочлен третей степени
(x7+x5+x4+x+1)
/ ( x3+x2+1)
Операция
деления может быть произведена или в виде
многочленов или в виде двоичных кодов.
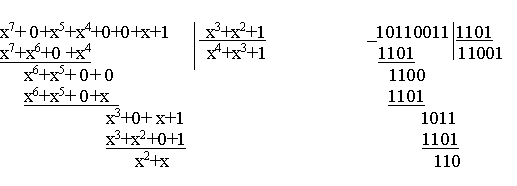
Схема деления реализуется на регистрах сдвига со встроенными сумматорами по модулю 2. Вид схемы определяется многочленом, на который производится деление. В процессе деления с помощью такого устройства находится остаток.
Пример
5.5.
Построить схему деления на многочлен
g(x)=x3+x+1
(1011)
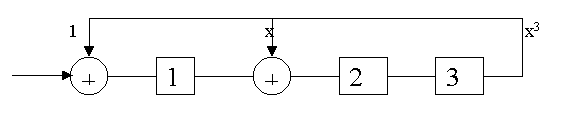
Рис.5.6.
Схема деления на многочлен
g(x)=x3+x+1
Пусть
на вход подается комбинация
10110001
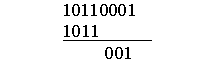
Процесс
деления
с помощью устройства показан в таблице
5.1.
Таблица
5.1
| Вх | 1 | |
3 |
| 1 | 1 |
0 | 0 |
| 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 0 | 0 |
0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 |
0 |
| 1 | 1 | 0 |
0 |
Циклический
код получают следующим образом: заданный
многочлен h(х)
сначала умножается на одночлен хn-k,
затем делится на образующий многочлен g(х).
В результате получим
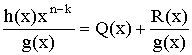 (5.3)
(5.3)
или
F(x) = Q(x) · g(x) = xn-kh(x) + R(X)
(5.4)
Таким
образом, циклический код можно построить
умножением кодовой комбинации h(х),
являющейся заданной, на одночлен хn-k
добавлением к этому произведению остатка R(х).
При декодировании, принятую кодовую
комбинацию необходимо разделить на g(x).
Наличие остатка указывает на ошибку.
Образующий
полином g(х)
является сомножителем при разложении
двучлена хn+1.
Сомножителями разложения двучлена
являются неприводимые полиномы (таблица
5.3).
Образующий
полином выбирают следующим образом. По
заданной кодовой комбинации k
определяют число контрольных символов из
соотношения
r
= log
(n
+ 1) или
по эмпирической формуле
r = [log{(k + 1) + [log(k + 1)]}]
(5.5)
Соотношение
значений n,
k,
r можно определить по таблице 5.2.
Таблица
5.2 зависимостей между n,
k
и r
| n | 3 | |
6 | 7 | 9...15 | |
33...63 | 65...127 |
| k | 1 |
2 | 3 | 4 | 5...11 | 12...26 | 27...57 | 28...120 |
| r | 2 | 3 | 3 | 3 | 4 | 5 | 6 | 7 |
Из
таблицы неприводимых полиномов (табл.5.3)
выбирают самый короткий многочлен со
степенью, равной числу контрольных
символов; его и принимают за образующий
полином.
Пример
5.6. Пусть
требуется закодировать комбинацию вида
1101, что соответствует h(х)
= х3 + х2 + 1.
По формуле (5.5) определяем число
контрольных символов r
= 3. Из таблицы 5.3 возьмем многочлен g(х)
= х3 + х + 1, т.е. 1011.
Решение:
Умножим
h(х)
на хr.
h(x)xr
= (x3 + x2 + 1)x3 = x6 + x5
+ x3 ®
11010000
Разделим
полученное произведение на образующий
полином g(х)
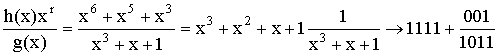
При
делении необходимо учитывать, что
вычитание производится по модулю 2.
Остаток суммируем с h(х)хr.
В результате получим закодированное
сообщение:
F(x)
= (x3 + x2 + 1) (x3 + x + 1) = (x3
+ x2 + 1)x3 + 1 ®
1101001
В
полученной кодовой комбинации
циклического кода информационные
символы h(х)
= 1101, а контрольные R(х)
= 001. Закодированное сообщение делится на
образующий полином без остатка.
Сообщение,
которое закодировано,
является
одной из
комбинаций 4-разрядного кода, так как
весь ансамбль сообщений (вся группа)
содержит N=16 сообщений. Это значит, что
если все сообщения передаются в
закодированном виде, то каждое из них
необходимо кодировать так же, как и
комбинацию h(x)
= 1101. Однако выполнять дополнительные 15
расчетов (а в общем случае 2n-k-1
расчет) нет необходимости. Это можно
сделать проще, путем составления
образующей (порождающей) матрицы.
Образующая
матрица составляется на основе единичной
транспонированной, к которой справа
дописывается матрица дополнений:
Hn,k
= || Ik,
Cn,r
||
(5.6)
Матрица
дополнений получается из остатков от
деления единицы с нулями на образующий
многочлен g(x).
Комбинации единиц с нулями представляют
собой векторы ошибок: 00...01, 00... 10, 00... 1...0 и т.д.
Каждому вектору ошибок будет
соответствовать свой остаток (опознаватель):

Получено
4 комбинации циклического кода, т.е.
столько, сколько информационных разрядов,
а так как в 4-разрядном двоичном коде
всего N
= 24 = 16 комбинаций, то остальные 11
ненулевых комбинаций находятся
суммированием по модулю 2 всевозможных
сочетаний строк образующей матрицы.
Например, необходимо из исходных кодов 1101
и 1010 получить циклические
помехозащищенные коды. Они получаются
суммированием соответствующих строк
образующей матрицы:
1.
1+3+4 = 1101001;
2.
2+4 = 1010011.