Передача информации по каналу связи. Пропускная способность канала 

Введение понятий энтропии, количества информации, скорости выдачи информации источником, избыточности позволяют характеризовать свойства информационных систем. Однако для сравнения информационных систем только такого описания недостаточно. Обычно нас интересует не только передача данного количества информации, но передача его в возможно более короткий срок; не только хранение определенного количества информации, но хранение с помощью минимальной по объему аппаратуры и т.п.

       Пусть количество информации, которое передается по каналу связи за время Т равно

  .  Если передача сообщения длится Т единиц времени, то скорость передачи информации составит  .

Это количество информации, приходящееся в среднем на одно сообщение. Если в секунду передается n сообщений, то скорость передачи будет составлять .

Пропускная способность канала есть максимально достижимая для данного канала скорость передачи информации:

                              (3.3)

Или максимальное количество информации, передаваемое за единицу времени: 

Скорость передачи может быть технической или информационной.

Под технической скоростью V_T, называемой также скоростью манипуляции, подразумевается число элементарных сигналов (символов), передаваемых в единицу времени   бод.

Информационная скорость или скорость передачи информации, определяется средним количеством информации, которое передается в единицу времени и измеряется  (бит/сек).  R=nH.

Для равновероятных сообщений составленных из равновероятных взаимно независимых символов  

В случае если символы не равновероятны 

В случае если символы имеют разную длительность

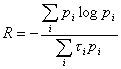                                                                                  (3.4)

Выражение для пропускной способности отличается тем, что характеризуется максимальной энтропией

 бит/сек

Для двоичного кода  бит/сек

Пропускная способность является важнейшей характеристикой каналов связи. Возникает вопрос: какова должна быть пропускная способность канала, чтобы информация от источника X к приемнику Y поступала без задержек?  Ответ на этот вопрос дает 1ая теорема Шеннона.

1.Теорема Шеннона

     Если имеется источник информации с энтропией Н(х) и канал связи с пропускной способностью С, то если С > H(X), то всегда можно закодировать достаточно длинное сообщение таким образом, что оно будет передано без задержек. Если же, напротив,   С < H(X), то  передача информации без задержек невозможна.

В любом реальном канале всегда присутствуют помехи. Однако, если их уровень настолько мал, что вероятность искажения практически равна нулю, можно условно считать, что все сигналы передаются неискаженными. В этом случае среднее количество информации, переносимое одним символом равно I(X,Y)=I(X,X)=H(X).   Максимальное значение  H_max=log m. Следовательно, пропускная способность дискретного канала без помех за единицу времени равна

  .

Реальные каналы характеризуются тем, что на каналы всегда воздействуют помехи. Пропускная способность дискретного канала с помехами вычисляется по формуле  C =n[H(Y)-H(Y/X)]_max .

Где средняя, условная энтропия со стороны приемника сигналов    

 А энтропия принимаемых сигналов определяется из условия максимального значения      H(y)= log m.

Пример 3.1. Пусть требуется определить пропускную способность бинарного канала связи. При этом с вероятностью p каждый из двоичных сигналов может перейти в противоположный сигнал.

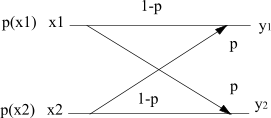
На рис.3.2  представлена  модель передачи бинарных сигналов

1-p  вероятность неискаженной передачи сигналов

   p  вероятность искажения сигналов

Рис.3.2.  Симметричный канал передачи сигналов в условиях помех, где x₁  и х₂  передаваемые сигналы типа “0” или “1”,   y₁ и y₂, принимаемые сигналы

   Матрица для нахождения условной вероятности  

                           y₁               y₂

Найдем полную  условную  энтропию системы y относительно x

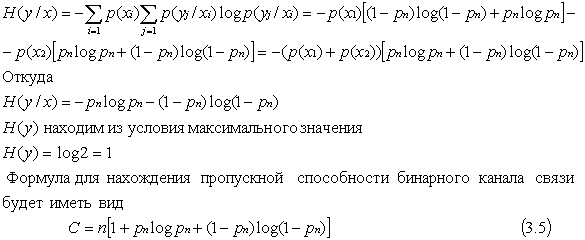
 График функции имеет следующий вид:                                        

 
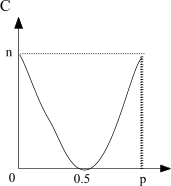        Наибольшее значение эта функция принимает                                     

       при p=0  (то есть при отсутствии помех)

     и при p=1  (то есть  при негативной передаче).        

        При  p=1/2 пропускная способность минимальна.  

            Рис.3.3. График функции  С=f(p)

Пример 3.2. Рассмотрим более общий случай передачи по дискретному каналу. Найдем пропускную способность m-ичного канала связи.

На рис. 3.4 представлена модель передачи m-ичных сигналов, где x₁,х₂,…,х_m источники информации, y₁,y₂,…,y_m приемники информации. 

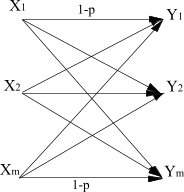
         Вероятность ошибки - p. Вероятность безошибочной передачи сигналов равняется 1- p, а в случае ошибки переданный сигнал может с одинаковой вероятностью (равной )быть воспринятым как любой из m-1 отличных от него сигналов.

Рис.3.4.  m-ичный канал передачи информации

Матрица  условных вероятностей имеет вид

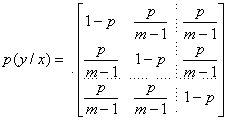
Полная  условная  энтропия системы Y относительно X

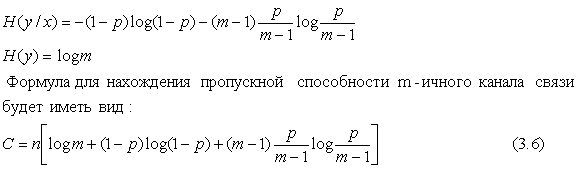
График функции С(p) пропускной способности канала связи при m=4 представлен на рис.3.5

             Рис.3.5. График функции C(p)

Эта функция максимальна при p=0,   при вероятности .     При     p=1    .  

Для дискретных каналов с помехами Шеннон дал вторую теорему.

           2. Теорема Шеннона.

Пусть имеется источник информации X, энтропия которого в единицу времени равна H(X), и канал с пропускной способностью C. Если H(X)>C, то при любом кодировании передача сообщений без задержек и искажений невозможна. Если же H(X)<C, то любое достаточно длинное сообщение  можно всегда закодировать так, что оно будет передано без задержек и искажений с вероятностью сколь угодно близкой к единице.