Основные теоремы кодирования   

Теорема 1. Неравенство Крафта.

 Неравенство является необходимым и достаточным условием существования кодовых слов, соответствующих концевым узлам дерева с длинами, равными k_j.

Теорема 2. Средняя длина кода  меньшая,  чем  является недостижимой ни при каком кодировании.

  Доказательство:

Покажем, что

  Теорема 3. Можно указать такой способ кодирования равно распределенных независимых сообщений, что средняя длина кода будет удовлетворять следующим требованиям:

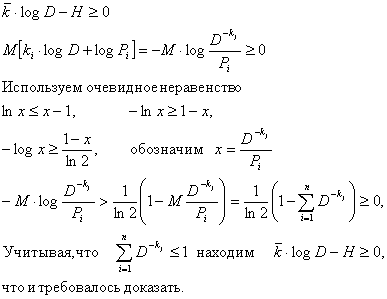
Доказательство.

Пусть D=2, M=20. В этом диапазоне заведомо имеется одно целое число

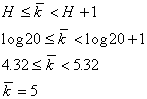
Теорема 4.  Существуют такие способы кодирования для достаточно длинного сообщения x₁, x₂, … , что средняя длина  кодового слова может быть сделана сколь угодно близкой к     .

Доказательство. Возьмем произвольное целое N>1 и разобьем последовательность x₁, x₂, … , на группы N случайных величин. Каждую такую группу будем рассматривать как одну случайную величину  Y=( x₁, x₂, … ,x_N) и применим к ней теорему (3).

,

где H_Y=NH_X ,   средняя длина слова, передающего сообщение  Y=( x₁, x₂, … ,x_N). Очевидно, что , тогда получим

Увеличивая N, Величину 1/N можно сделать сколь угодно малой, что доказывает теорему.