Код Хаффмана

Второй код, являющийся не менее эффективным, чем код Шеннона-Фано, является код Хаффмана. Он также учитывает статистические свойства сигналов, при которых вероятности появления букв p₁, р₂, …р_к не равные между собой, поэтому H < log n.

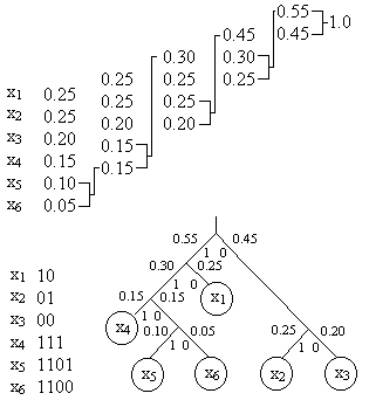
Код Хаффмана строится следующим образом: буквы располагают в порядке убывания их вероятностей. Складывают вероятности двух последних букв, и ряд переписывают снова с учетом новой вероятности (суммы). Далее повторяют операцию, пока не получится 1. Нижнюю букву всегда кодируют нулем, а верхнюю – единицей.

Для составления кодовых комбинаций строится кодовое дерево. Двигаясь по кодовому дереву сверху вниз, можно записать для каждой буквы соответствующую ей кодовую комбинацию.

Код Хаффмана, также как и Шеннона-Фано является префиксным, то есть в таком коде ни одна комбинация не совпадает с началом более длинной комбинации, а это позволяет обеспечить однозначное декодирование без введения разделительных символов.

Среднее кол-во разрядов:

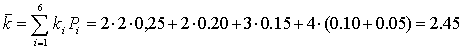
Энтропия

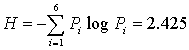
Как мы видим, величина среднего кол-ва разрядов получилась достаточно близкой к энтропии, следовательно, код можно считать эффективным. При этом для сравнения можно вычислить величину K для равномерного кода: