Вопросы

4.1. Какие коды позволяют производить однозначное декодирование даже без пробела? Приведите примеры таких кодов.

4.2. До какого предела может быть уменьшена средняя длина кодовой комбинации?

4.3. Назовите условия построения оптимальных кодов.

4.4. Сформулируйте основные теоремы кодирования.

4.5. С какой целью используются эффективные коды, и какие из них Вам известны.

4.6. Назовите причины использования  блочного кодирования.

4.7. Перечислите основные методы сжатия информации.

4.8. Как осуществляется сжатие методом лексического кодирования?

Упражнения

4.1 Сообщения составляются из букв алфавита а, b, с, d. Вероятности появления букв алфавита в текстах равны соответственно 0,2; 0,3; 0,4; 0,1. Найдите избыточность сообщений, составленных из букв данного алфавита.

Решение.

Для алфавита из четырех букв максимальная энтропия составит  H_max = log m = log 4 = 2. Средняя энтропия на символ сообщения 

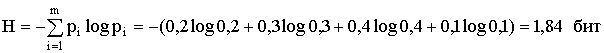
Тогда избыточность D = 1 - H/H_max = 1-1,84/2 = 0,08.

4.2. Закодируйте кодами Шеннона-Фано и Хаффмена алфавит, состоящий из пяти букв, - а1, а2, а3, а4, а5, вероятности появления которых Р = 0,4; 0,3; 0,15; 0,1; 0,05.

Решение.

Построение кода Шеннона-Фано иллюстрируется на рис.У.1.  

Рис. У.1. Построение кода Шеннона-Фано 

Определим, какова эффективность полученного кода. Для этого подсчитаем среднее число символов, приходящихся на букву: 

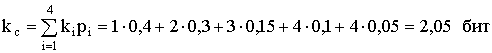
Энтропия  

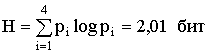
Таким образом, средняя длина  получилась достаточно близкой к предельному значению. Длина кода при равномерном кодировании k = 3 бита. Код Шеннона-Фано по сравнению с равномерным кодированием позволил сократить среднюю длину кодовых комбинаций для данного примера на 31,6%. D = 1- 2,05/3 = 0,316.  

Рис.У.2. Построение кода Хаффмена. 

Средняя длина кода k_c = 2,05 бит совпала с длиной, полученной по методике Шеннона-Фано.

4.3. Закодируйте двоичным кодом Шеннона-Фано ансамбль сообщений Х = х1, х2, ..., х8, если все кодируемые сообщения равновероятны. Показать оптимальный характер полученного кода.

4.4. Определите количество элементов в кодовом слове, если известно общее число комбинаций N = 512, а основание кода 2.

4.5. Сколько двоичных чисел может быть представлено 7-разрядным кодом?

4.6. Дана совокупность символов х1, х2, х3, х4 со следующей статистикой соответственно: 0,28; 0,14; 0,48; 0,10. Закодируйте символы по методу Шеннона-Фано и определите эффективность кода.

4.7. Имеется статистическая схема сообщения  

Произведите кодирование отдельных букв и двухбуквенных сочетаний по методу Шеннона-Фано, сравните коды по их экономичности (количество информации, приходящееся на один символ) и избыточности.

4.8. Сообщение состоит из последовательности двух букв А и В, вероятности появления каждой из которых не зависят от того, какая была передана раньше, и равны 0,8 и 0,2 соответственно. Произведите кодирование по методу Шеннона-Фано: а) отдельных букв; б) блоков, состоящих из двухбуквенных сочетаний; в) блоков, состоящих из трехбуквенных сочетаний. Сравните коды по их экономичности.

4.9. Дана совокупность символов Х со следующей статистической схемой: 

 Произведите кодирование двоичным кодом по методу Хаффмена и вычислите энтропию сообщения Н(Х) и среднюю длину кодового слова.

4.10. Пусть алфавит А содержит 6 букв, вероятности которых равны 0,4; 0,2; 0,2; 0,1; 0,05 и 0,05. Произведите кодирование кодом Хаффмена. Вычислить энтропию сообщений Н(Х) и среднюю длину кодового слова.

4.11. Источник информации выдает сообщения со скоростью R = 1000 символов/с. Алфавит состоит из 3 символов (букв) X, Y, Z, статистика появления которых равна 0,7; 0,2; 0,1. Закодируйте  символы источника информации таким образом, чтобы обеспечить прохождение сообщений через канал связи с пропускной способностью С = 1250 бит/с без задержек.